大逆不道,从天界偷下来的算法修仙秘籍竟然传到你手上~~(结尾有彩蛋)
大逆不道,从天界偷下来的算法修仙秘籍竟然传到你手上~~(结尾有彩蛋)
这有可能是你见过最离谱的标题
这有可能是你没见过的技术文章模式
我不知道我的选择是否正确,但是我的想法就是:
不再让技术冷冰冰,让所有人学习中获得快乐!
序言
这是一个奇妙的世界,
本来人们在这个世界上相处融洽,大家互相包容,没有任何制度……
人们在这个世界上感受到了一丝丝的温馨幸福,
但是反而到来的是制度的缺失导致的无畏纷争和内心世界极大的空虚~~
但是突然的一天,这一切都她被改变了,
她,来自天界,一个身穿天青色长裙的仙女,
拥有一种神秘的功法能让本来复杂性的工作大大缩短时间;
而且之前常用的大型机器设备,也通过她的改造竟然用一台小而精妙的工具就能实现,大大减少了空间;
有些人偷看女子施法,竟然发现这种功法就是在一个只有26个按键机器上行云流水的反复敲打,
这是因为如此惊人的工作效率,有些志气风发的少年决定向她学习这种功法,
但是当仙女见到这些少年,都是摇摇头,说着:不具备这种天赋。
当到最后一个少年,仙女还是摇了摇头说:“不行!”
最后的他竟然没有离去,冒着“大不敬”出口就说:“难道你说不行就不行,我们的人生由我们自己努力,不是你在上面摇摇头就能否定我们一生的价值与意义,我的人生有我们自己定义,而不是你!”
仙女大为震惊,世间竟然能有如此气魄的少年,他也是古今第一人了。
于是仙女收他为徒,得知这种功法名为算法,在传授算法技巧,不出几年这位少年就成为大修行者
但是距离突破天境还差一步,因为还没有得到算法心法的传授
根据天界规则不许将心法传授给凡人,
但是少年不希望这种功法一直被天界人掌控,希望他能被每一个人掌握,人们生来平等都有受教育的权利。
于是他趁着仙女去天界拜寿以奴婢的身份把心法偷出了天界
还没等到世间,就被天界的人围追堵截,情急之下,把心法用尽全身的力气抛到人间
这本心法刚好砸到了正在晒太阳的你,你看到这本书还不知是什么
于是就开始翻阅~~~
第一章 | 初识算法之复杂度
学习数据结构与算法的第一歩,永远都是复杂度分析
复杂度分析
毫不夸张的说,这就是数据结构与算法学习的内核所在。
你学会了它你就登堂入室,封侯拜相,
你学不会它,你就永远是孤苦伶仃的卖炭翁!(会背的小伙伴可以吟诵起来啊)

那你就会问我,为什么复杂度分析会这么重要?
我们平常工作摸鱼的时候,总是想着当当咸鱼划划水老板的钱就能钻进我的卡里,
更好就是能泡个澡按个脚睡个觉,每天就有工资领~~
(嘻嘻嘻,年轻人不要幻想了,小心被洗脚水淹到哦)
数据结构与算法虽然没有我们有这么大的梦想,
但是它的出现也是想着花更少的时间和更少的存储来解决问题。
一句话————花少钱办大事
那如何去考量“更少的时间和更少的存储”,用来衡量时间和储存的量度复杂度分析为此而生。
事后统计法
概括
那肯定有同学出来反驳说:现在有很多工具啊包啊,代码随便跑一下,就能轻轻松松知道运行了多少时间占了多少内存啊。算法的效率不就轻松比对出来了么?
这种方法就是我们常说的事后统计法,
那边都已经写完代码了,你之后统计知道了,那我要你跑出效率图像还个屁用,
类似于前段时间B站崩溃事件,我知道那块JS代码部分忽略了字符串”0”的注入导致时间复杂度剧增,
导致服务器瘫痪了,写代码的时候就测出来了,那样还会耽误我看舞蹈区,额呸,知识区来学习吗
简单来说,就是你需要提前写好算法代码和编好测试数据,然后在计算机上跑,通过最后得出的运行时间判断算法时效的高低,这里的运行时间就是我们日常的时间。
缺点
首先,事后统计法太依赖计算机的软件和硬件等性能。
再者,事后统计法太依赖于测试数据集的规模。
结果
可以看出,
我们需要一个不依赖于性能和规模等外力影响就可以估算算法效率、判断算法优劣的度量指标,
而复杂度分析天生就是干这个的,这也是为什么我们要学习并必须学会复杂度分析!
时间复杂度
时间复杂度,也就是指算法的运行时间。
对于某一问题的不同解决算法,运行时间越短算法效率越高,相反,运行时间越长,算法效率越低。
那么如何估算时间复杂度呢?
当用运行时间去描述一个算法快慢的时候,算法中执行的总步数显得尤为重要。
因为只是估算,我们可以假设每一行代码的运行时间都为一个 Btime,那么算法的总的运行时间 = 运行的总代码行数。
下面我们来看这么一段简单的代码。
1 | def dogeggs_sum (n): |
这段求累加和的代码总的运行时间是多少呢?
第 2 行代码需要 1 Btime 的运行时间,第 4 和 第 5行分别运行了 n 次,所以每个需要 n * Btime 的运行时间,所以总的运行时间就是 (1 + 2n) * Btime。
我们一般用 T 函数来表示赋值语句的总运行时间,所以上面总的运行时间就可以表达成 T(n) = (1 + 2n) * Btime,翻译一下就是“数据集大小为 n,总步数为 (1 + 2n) 的算法的执行时间为 T(n)”。
通过公式,我们可以看出 T(n) 和总步数是成正比关系,这个规律的发现其实是很重要的,因为这个告诉了我们一种趋势,数据集规模和运行时间之间有趋势!
大 O 表示法
大 O 表示法,表示的是算法有多快。
这个多快,不是说算法代码真正的运行时间,而是代表着一种趋势,一种随着数据集的规模增大,算法代码运行时间变化的一种趋势。一般记作 O(f(n))。
那么之前的公式就变成 T(n) = O(f(n)),其中 f(n) 是算法代码执行的总步数,也叫操作数。
n 作为数据集大小,它可以取 1,10,100,1000 或者更大更大更大的数,到这你就会发现一件很有意思的事儿,那就是当数据集越来越大时,你会发现代码中的某些部分“失效”了。
还是以之前的代码为例。当 n = 1000 时,1 + 2n = 2001,当 n = 10000 时,1 + 2n = 20001,当这个 n 持续增大时,常数 1 和系数 2 对于最后的结果越来越没存在感,即对趋势的变化影响不大。
所以对于我们这段代码样例,最终的 T(n) = O(n)。
如果 T(n) = O(n) + O(n²) + O(n³),按照我们取“主导”部分,显然前面两个小弟都应该直接 pass,最终 T(n) = O(n³)。
对于时间复杂度分析来说,只要找起“主导”作用的部分代码即可,这个主导就是最高的那个复杂度,也就是执行次数最多的那部分 n 的量级。
常见时间复杂度
算法学习过程中,我们会遇到各种各样的时间复杂度,但纵使你代码七十二变,几乎也逃不过下面这几种常见的时间复杂度。
| 时间复杂度 | 阶 | f(n) 举例 |
|---|---|---|
| 常数复杂度 | O(1) | 1 |
| 对数复杂度 | O(logn) | logn + 1 |
| 线性复杂度 | O(n) | n + 1 |
| 线性对数复杂度 | O(nlogn) | nlogn + 1 |
| k 次复杂度 | O(n²)、O(n³)、…. | n² + n +1 |
| 指数复杂度 | O(2n) | 2n + 1 |
| 阶乘复杂度 | O(n!) | n! + 1 |
空间复杂度
空间复杂度和时间复杂度一样,反映的也是一种趋势,只不过这种趋势是代码运行过程中临时变量占用的内存空间。
代码在计算机中的运行所占用的存储空间呐,主要分为 3 部分:
- 代码本身所占用的
- 输入数据所占用的
- 临时变量所占用的
前面两个部分是本身就要占这些空间,与代码的性能无关,所以我们在衡量代码的空间复杂度的时候,只关心运行过程中临时占用的内存空间。
空间复杂度记作 S(n),表示形式与时间复杂度一致。
在这同样 n 作为数据集大小,f(n) 指的是规模 n 所占存储空间的函数。
空间复杂度分析
下面我们用一段简单代码来学习下如何分析空间复杂度。
1 | def dogeggs_sum(lst): |
上述代码是求列表 lst 的所有元素之和,根据之前说的,只计算临时变量所占用的内存空间。
形参 lst 所占的空间不计,那么剩下的临时变量只有 sum 和 i,sum 是存储和,是常数阶,i 是存储元素位置,也是常数阶,它俩所分配的空间和规模 n 都没有关系,所以整段代码的空间复杂度 S(n) = O(1)。
第二章 | 初探数据结构—数组-至纯之物
含义
数组是一种基础的线性数据结构,它是用连续的一段内存空间,来存储相同数据类型数据的集合。
这里面有两个重点:
- 线性数据结构
- 连续内存存储相同数据类型
线性结构
线性数据结构有限的,它是某类元素的集合并且记录着元素之间的一组顺序关系,除了首尾之外,其余元素之间有且只有一个前驱和后继。
除了数组以外,像单链表、栈、队列等也是典型的线性数据结构。
连续内存存储的相同数据类型
以一个长度为 6 的 int 类型的数组为例,理解一下“连续内存存储相同数据类型”数组的样砸。
上图中的计算机给数组 a 分配了一块连续的内存空间 1000 - 1005,首地址 address[0] = 1000。
因为连续,且对于数组来说下标从 0 开始的,所有对于数组中的每个元素来说,它的内存地址就很好计算:
1 | address[i] = address[0] + i |
数组的操作
从上面可以看出,连续内存存储使得数组有一个天然的优势,这个优势就是可以根据下标,快速的随意访问任意一个位置的数组元素。
查找
因为数组可以保证不管你访问哪个元素,只要给出下标,只需进行一次操作,就可以定位到元素的位置,从而拿出这个位置上的值。
这步操作的时间复杂度就是 O(1)。
连续的内存使得在插入或者删除的元素的时候,其它元素也要相应的移动。
插入
比如我们在下标为 2 的位置上插入一个元素 29:
为了保持连续内存存储,在下标为 2 的位置上插入 29,原先 2 - 5 下标位置上元素都要向后一步走,可以看出这一步操作的时间复杂度为 O(n)。
一般我都是按照最坏情况时间复杂度来算。对于插入来说,最好的情况肯定是插在末尾,这样所有的元素都不用动,时间复杂度为 O(1),那最坏的情况就是在数组的开头插入,这样所有的元素都要动,时间复杂度就成了 O(n),请大家一定要注意。
删除
对删除来说,和插入操作也差不多,比如我们删除下标为 2 位置上的元素。
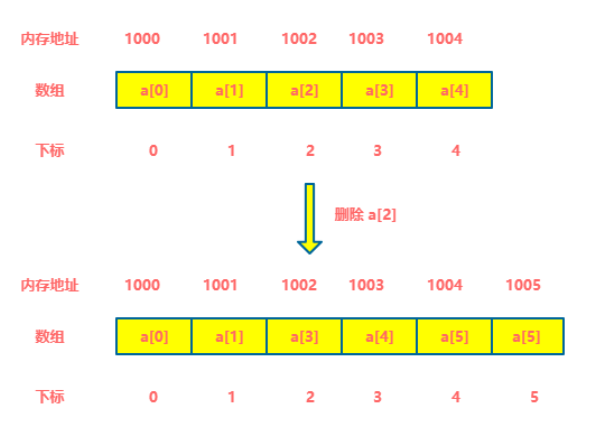
删除了下标 2 位置上的数字 a[2], 原来下标 3 - 5 位置上的元素统统向前一步走。
同样对于删除来说,最好情况是删除末尾的元素,时间复杂度为 O(1),最坏的情况是删除首位的元素,时间复杂度是 O(n)。
特别注意
在做数组类问题的时候要注意数组越界的问题。
数组越界,简单来说就是对于一个大小为 n 的数组,它的下标应是 0 到 n-1,对这 n 个位置的元素之外的访问,就是非法的,这就叫做“越界”。
第三章 | 初探数据结构—链表-长而简之
出现缘由
第二章 | 初探数据结构—数组的文章中说过,连续的内存使得数组在进行插入和删除时需要移动大量元素,这就意味着要耗费时间。
相比于数组,链表操作是可以缩稍时间,但是也是复杂一些的数据结构。
定义
线性表的链式存储结构生成的表,叫做链表。
那么什么是链式存储结构咧?
链式存储结构是指用一组任意的存储单元存储线性表的数据元素,通过指针连接串联起来。
这里的“任意”指的就是,存储单元可以连续也可以不连续,这就意味着它们可以是内存中任何未被占用的地方。
链表中的存储单元叫做节点。它和数组中只存数据信息不同,每个节点分为两部分:数据域和指针域。数据域存储的数据,指针域存储着同一个表里下一个节点的位置。
因为链表家族里的兄弟姐妹太多,在这里咧我只讲常见的几种链表结构:单链表、双向链表。
单链表
单链表是一种通过指针串联在一起的线性结构,每一个节点由两部分组成,一个是数据域一个是指针域(存放指向下一个节点的指针),最后一个节点的指针域指向null(空指针的意思)。
链接的入口节点称为链表的头结点也就是head。
如图所示: 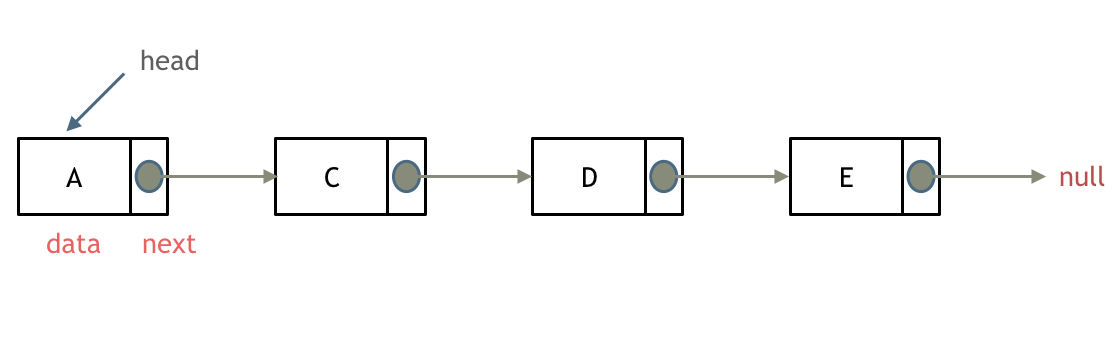
双链表
单链表中的指针域只能指向节点的下一个节点。
双链表:每一个节点有两个指针域,一个指向下一个节点,一个指向上一个节点。
双链表 既可以向前查询也可以向后查询。
如图所示: 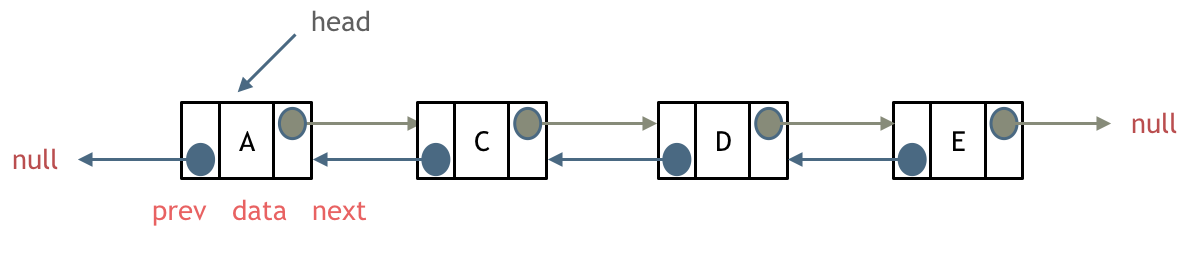
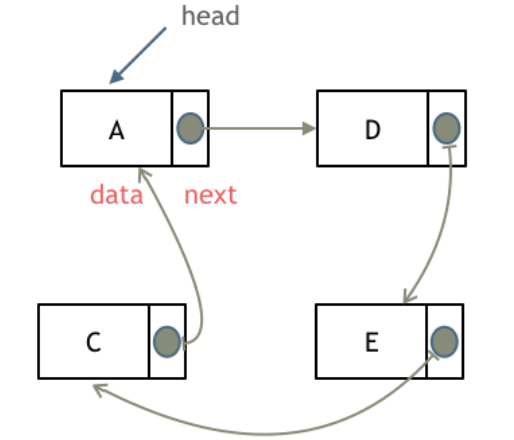
循环链表
循环链表,顾名思义,就是链表首尾相连。
循环链表可以用来解决约瑟夫环问题。
链表操作
删除节点
删除D节点,如图所示:
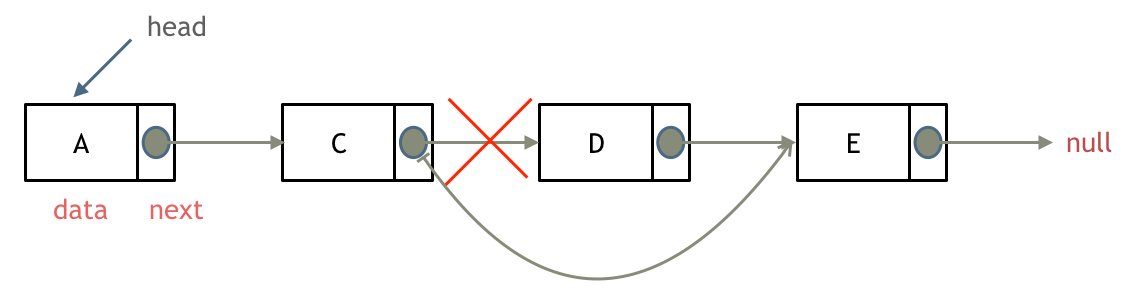
只要将C节点的next指针 指向E节点就可以了。
那有同学说了,D节点不是依然存留在内存里么?只不过是没有在这个链表里而已。
是这样的,所以在C++里最好是再手动释放这个D节点,释放这块内存。
其他语言例如Java、Python,就有自己的内存回收机制,就不用自己手动释放了。
添加节点
如图所示:
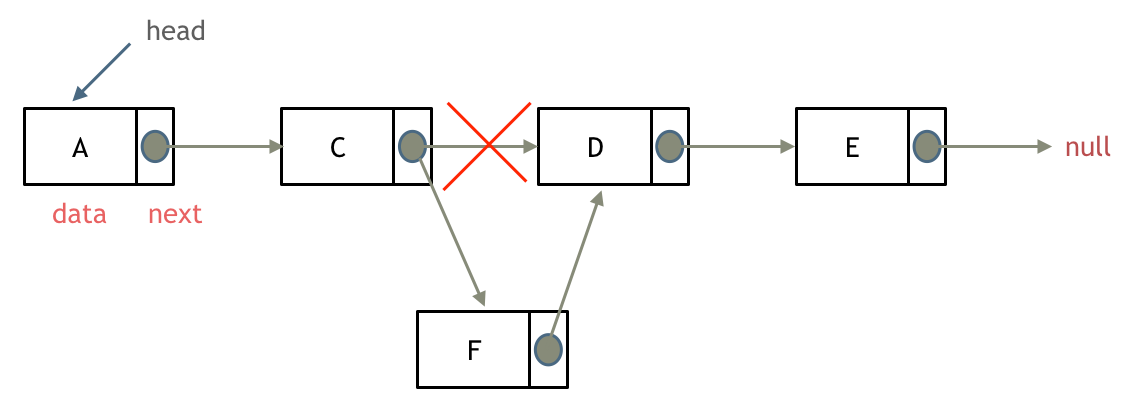
可以看出链表的增添和删除都是O(1)操作,也不会影响到其他节点。
但是要注意,要是删除第五个节点,需要从头节点查找到第四个节点通过next指针进行删除操作,查找的时间复杂度是O(n)。
性能分析
再把链表的特性和数组的特性进行一个对比,如图所示:
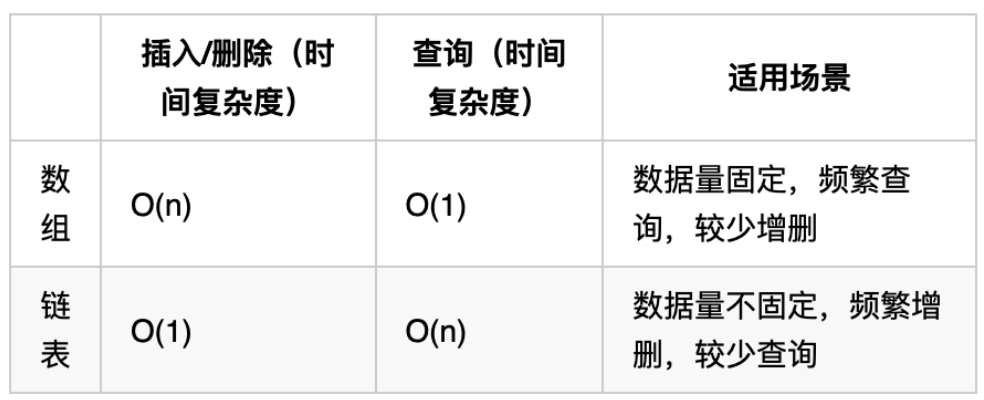
数组在定义的时候,长度就是固定的,如果想改动数组的长度,就需要重新定义一个新的数组。
链表的长度可以是不固定的,并且可以动态增删, 适合数据量不固定,频繁增删,较少查询的场景。
第四章 | 初探数据结构—哈希表-杂而不乱
出现缘由
要查一个数在数组中的位置,那可是太费劲了,只能从头开始一个个的比较,直到找到相等的才算完事。
这个方法,说实话也太笨了,简直不是我这种懒人应该做的事。
就不能有种方法直接看到这个数,就直接在数组中查到位置嘛?!
诶,你别说,还真有。
因为总有比我更懒的,我只是懒是只能躺着,人家大佬的懒是直接动手解决,果然那句”懒是第一生产力“!
定义
这个就是我今天要给家人们带来的哈希表。
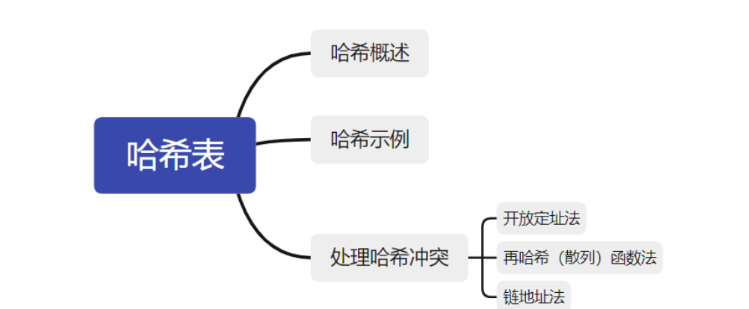
哈希表,别名儿叫散列表(Hash Table)。
我在上面说,希望有种方法,直接看到数,就知道它在数组中的位置,其实里就用到了哈希思想。
哈希思想就是说不用一些无用的比较,直接可以通过关键字 key 就能找到它的存储位置。
这里举一个栗子(可不是堂嫂栗子哦),可能更清楚点:
智能班有 40 个学生,每个学生的学号由入学年份 + 年级 + 班级 + 编号组成,例如 2020.20.01.32 是 2020 年入学的 20 级 01 班的 32 号同学。(学号怕你看混,给你个”.”分割,贴心不~)
现在有个需求(烦人的 PM):我们需要快速找到某个同学的个人信息。
那这个时候我们就要建立一张表,按理来说我要是想要知道某个同学的个人信息,其实就知道学号就好了,但是在这不行,学号的值实在太大了,我们不能把学号当作下标。
学号不可以,那什么可以呢?我们定睛一看,咦,编号可以呀,编号是从 1 ~ 40。(我真是一个小聪明啊)

那咋取到编号?不就是学号对 2020.20.01.00 取余就 KO 了嘛。(你不会没理解把,不就是相当于(上面栗子 32 这位大帅哥),32/00=32 嘛)
此时,如果我们想查学号为 2020.20.01.32 的学生个人信息,只要访问下标为 32 的数据即可。
其实这就可以在时间复杂度为 O(1) 内解决找到。(不要问我什么是时间复杂的,什么是空间复杂度,生产队的 LV 马上更,不要打拉)
秒男实锤了。(这摸快,O(1),比三秒都快哦)

用公式表示就是:**存储位置 = f(关键字)**。
这里的 f 又叫做哈希函数,每个 key 被对应到 0 ~ N-1 的范围内,并且放在合适的位置。
在上面的例子中 f(key) = key % 2021210100。
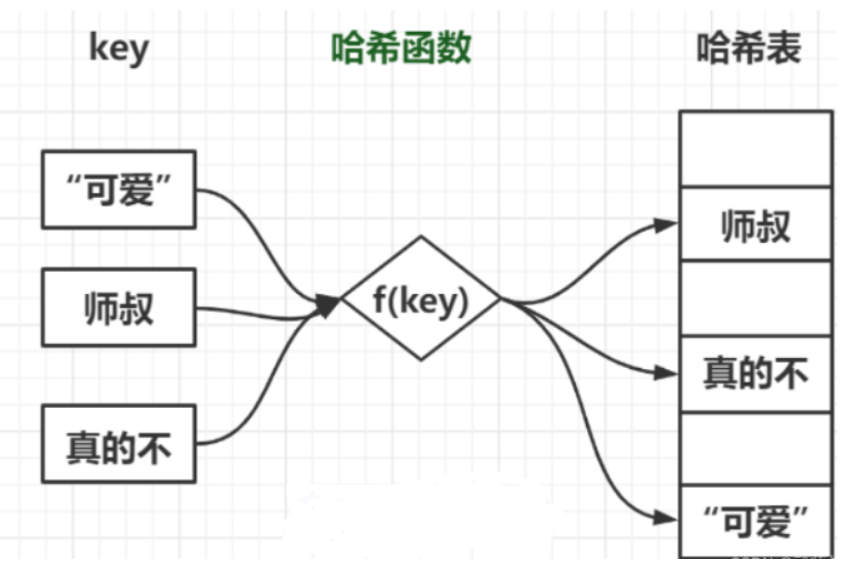
存储时,通过同一个哈希函数的计算 key 的哈希地址,并按照此哈希地址存储该 key。
最后形成的表就是哈希表,它主要是面向查找的存储结构,简化了比较的过程,提高了效率。
示例
上面看明白的话,那再举个大栗子加深点印象。
有个 n = 10 的数组,哈希函数 f(key) = key % 10,将 4,10,11,19,29,39 散列到数组中。
哈希函数确定后,剩下的就是计算关键字对应的存储位置。
4 % 10 = 4,所以将 4 放入下标为 4 的位置。

10 % 10 = 0,所以将 10 放入下标为 0 的位置。

11 % 10 = 1,所以将 11 放入下标为 1 的位置。

19 % 10 = 9,所以将 19 放入下标为 9 的位置。

29 % 10 = 9,所以将 29 放入下标为 9 的位置。
但是现在问题来了,下标为 9 的这个坑已经被 19 占了,这 29 计算出来的下标冲突了。(作为工具人的我,呜呜,就让我为你来平定冲突和亲去,昭君我来了)

这种情况有个学名,叫:哈希(散列)冲突。
处理冲突
对于两个不相等的关键字 key1 和 key2,若 f(key1) = f(key2),这就是哈希冲突。
key1 占了坑,那 key2 只能想别的办法,啥办法呢?
一般处理哈希冲突有以下几种办法:
- 开放定址法
- 再哈希(散列)函数法
- 链地址法
- 。。。(别想了,就等你来创造一个,作为算法“行业冥灯”,击垮他们!)
开放定址法
一旦发生冲突,就选择另外一个可用的位置。
开放定址法有 2 个最常用的策略:
- 线性探测法
- 二次探测法
线性探测法
线性探测法,顾名思义,直来直去的探测。
且看它的公式:
f(key) = (f(key) + di) % m (di = 1, 2, 3, … , m-1)。
我还是用“哈希示例”中的栗子(栗子都快熟了):
n = 10 的数组,哈希函数 f(key) = key % 10,将 4,10,11,19,29,39 散列到数组中。

到了 29 的时候,29 % 10 = 9。
但此时下标 9 已经有了元素 19,所以此时探测下一个位置 (9 + 1) % 10 = 0。
下标为 0 的位置上已经有了元素 10,所以继续探测下一个位置 (9 + 2) % 10 = 1。
下标为 1 的位置上也有了元素 11,所以还得继续探测下一个位置 (9 + 3) % 10 = 2。
下标为 2 的位置上总算是空的,因此 29 找到了家(我家的猫不会跳舞,但是会爬树):

不知道你发现了没,对于 29 这个来说,本来只是和 19 冲突,整着整着和 10,11 也冲突了。
这样就使得每次要处理好几次冲突,而且这样会出现大量数字聚集在一个区域的情况,大大降低了插入和查找的效率。
后来不知道哪个大佬在线性的基础上做了改进,捣鼓出二次探测法。
二次探测法
二次探测法就是把之前的 di 整成了平方,公式如下:
f(key) = (f(key) + di) % m (di = 1², -1², 2², -2², …, q², -q², q ≤ m/2)
比如对于 29 来说,下标为 9 的位置上呆了 19,所以此时探测下一个位置 (9 + 1²) % 10 = 0。
下标为 0 的位置上占了元素 10,那下一次就探测上一个位置 (9 - 1²) % 10 = 8。
下标为 8 的位置上空着,直接占住:

再哈希函数法
再哈希的话,就是不只是一个哈希函数,而是使用一组哈希函数 f1(key)、f2(key)、f3(key)….。
当使用第一个哈希函数计算到的存储位置被占了,那就用第二个哈希函数计算,反正总会有一个散列函数能把冲突解决掉。
依次类推,直到找到空的位置,然后占住。
当然这种方法不会出现大量数字聚集在一个区域的情况,但这种情况明显增加了计算的时间。
链地址法
是谁说出现冲突后只能找别的坑位的,几个人蹲一个坑它不香嘛。(还记得伦敦的谜语吗)

可能真的有巨佬觉得香,然后就整出了链地址法。
链地址法呢是将得出同一个结果的 key 放在一个单链表中,哈希表存储每条单链表的头指针。
还是用老栗子:n = 10 的数组,哈希函数 f(key) = key % 10,将 4,10,11,19,29,39 散列。
最后得到如下图:
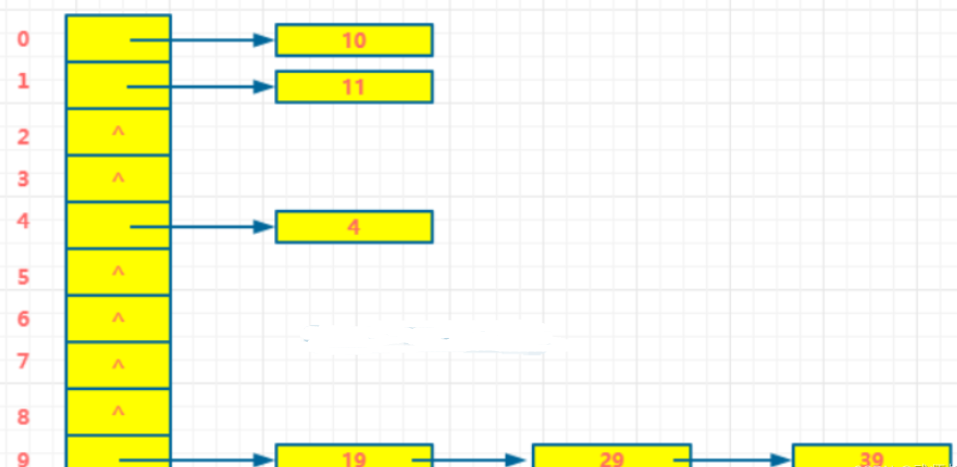
你看,链地址法就不会出现此坑被占,就得去找别的坑的情况。
大家一起蹲,这样就绝不会出现找不到地址的情况,而是直接插到对应的单链表中即可,所以**插入的时间复杂度为 O(1)**。
当然有得必有失,这样的情况必然造成了查找上的性能损耗,这里的查找的时间复杂度为 O(k),其中 k = n / 单链表条数。
第五章 | 初探数据结构—字符串-
敬请期待~~~
写在结尾[彩蛋大放送]
首先非常感谢InfoQ 携手阿里云打造写作培训课程,助力第三季InfoQ 百位优质创作者签约计划
在这里看到了很多优秀创作者大佬分享自己的独特经验,我竟然和自己的偶像[B站UP]三太子敖丙
一起连麦聊了一会,同时也解答了我对敖丙开发转运营一直以来的困惑~~
很高兴大家能看到这里,
其实文章写到你可能感觉这篇文章好混乱,
有我命由我不由天的大格局,有幽默的荤段子,有工作中的小调侃,有小小的自嘲,有历史重现……
诸多元素的在技术文章的奇妙碰撞,也独有一番风味;
突然写到结尾就有了一些感慨,
这让我想到了前段时间infoQ送给优秀开发者的T恤——极客青年

还请忽略师叔的小肚子,其实之前我一直以为这几个字比较呆版,
但是他点醒了我,极客是我们的工作,
但是重点我们还是青年,我们可能技术不是大佬,但是我们都有一个共同点热爱分享技术!
正式因为我们 share and love (分享热爱)

通过我们的每一篇文章在某一刻在启发正在疑惑的年轻人
也许我很微小,文章很浅薄,但是我还是青年
而且我还有你们,同为社区开发者的道友
就让你我用奇思妙想来分享属于技术
让技术变得有湿度
让技术变得有爱
最后让“极客青年”的我们,通过社区的方式,共同努力帮助更多的伙伴们!









